I easily spent the most time during development on the scissors tool, which might be surprising given how simple it is to use. You can see a quick example below. Just like real scissors, you can easily slice your pictures into any shape.
It seems simple enough right, so what makes this so tough? The next example shows just how robust the scissors are. For a dramatically bizarre shape, they still cut it into pieces just as you’d expect, and quickly at that. And it even supports cutting holes into scraps too.
We’re getting closer to seeing why this is so tough: it’s cutting arbitrary shapes with an arbitrary path into an arbitrary number of sub-shapes or holes, and doing this quickly enough on a relatively small mobile processor.
First: The Model
Before we can dive into how the slice happens, we have to understand how the data is modeled.
Each scrap is at least is a closed (looped) outer Bézier path with potentially many inner paths. Each of those Bézier paths is actually made up of many segments, each of which is a single cubic Bézier curve. Following along these path elements shows up the direction of that path. The enclosed subpaths are always in the reverse direction of the outer shape path.
You can see an arbitrary shape here, along with its numbered segments and path direction. Next to it is a simple 3 segment scissor cut.
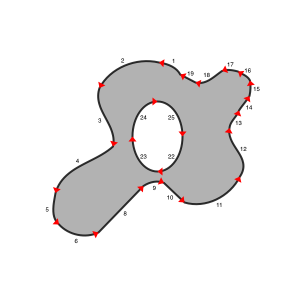
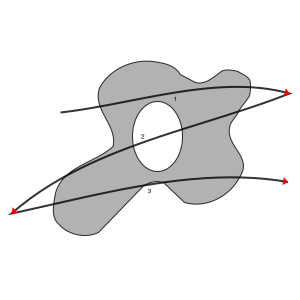
With only these two paths, we can determine how to cut the original shape into its smaller pieces.
Second: The Algorithm
In the picture above, it’s obvious to us humans where the new scraps would be, but for a computer to calculate the new shapes, it has to detect where the shape’s path and the scissor’s path intersect. This gives us the key pieces that show which segments of the scissor’s line will be edges of new subshapes, and which pieces we can safely ignore.
Once we find these intersection points, we can throw away all pieces of the scissors that aren’t inside of the shape. Next we compile a list of all segments of the shape, their direction, and the intersecting segments of the scissors, and their direction. The scissors’ segments are special, and we duplicate these, one for each direction.
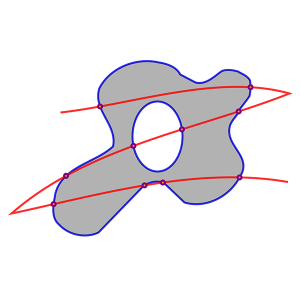
After all of this path processing, we’re finally ready to calculate the paths of our new sliced shape!
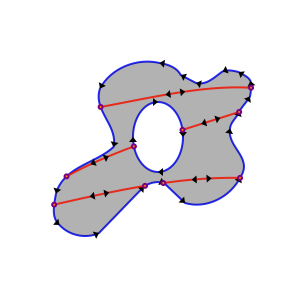
Now we follow these simple rules:
- each of the shape’s segments can be used only once
- pick any of the scissor segments of either direction
- follow it along its direction to the next intersection
- follow the arrows, turning left at each intersection, until you reach the original segment again
- continue until you run out of segments to use
Third: The Output
Tracing along the edges in this way, and you’ll easily compile up a list of the new shapes.
Fourth: Debugging
The real difficulty of this process came from a number of reasons:
- The UIBezierPath class for iOS is extremely lacking, especially when compared to NSBeizerPath in OS X
- There are no built in methods to find intersection points or splitting of Bezier paths or curves
- By default, accessing any element of a UIBezierPath requires looping through the entire path, making most any algorithm performance terrible
All of that means that I needed to write lots of Bezier specific code, which generally means lots of bugs too.
I used unit tests to verify as much of my code as I could, but it was very had to catch every edge case – especially when the scissors and shape would be at tangents. To help find these edge cases, I also write a small iOS app that’d let me draw any shape and then cut it with any scissor path. This let me try new shapes and cuts extremely quickly – I even gave the app to my 5yo daughter and asked her to try and break it.
Anytime the app threw an exception or otherwise had a problem – it would email me the paths of the shape and scissors for me to debug and add to my unit tests. In this way, I slowly built up a library of unit tests as I worked toward a robust solution.
Fifth: References
For anyone looking to write code for Bezier paths, I highly suggest the following reading and resources:
- A Primer on Bézier Curves – http://pomax.github.io/bezierinfo/
- KevinLinDev Geometry Tutorial – http://www.kevlindev.com/gui/math/polynomial/
- DrawKit – http://apptree.net/drawkit.htm